Great Circles and Ham Sandwiches

Today we will digress from the theme of our recent posts and discuss some interesting geometric truths that your grandmother might even find interesting. To whet your appetite, consider the following claim:

There are always 2 opposite points on the Earth's equator that have exactly the same temperature.

It has been known for millennia that the Earth's shape can be approximated by a sphere. Greek philosophers as early as Pythagoras made claims of the Earth's spherical shape. Perhaps the most notable arguments from antiquities for a spherical Earth were given by Aristotle who observed, among other things, that the Earth cast a round shadow on the Moon during a lunar eclipse.

By the Hellenistic era (~300BC), the spherical Earth hypothesis was an established given. Moreover, the circumference of the Earth was estimated (with astounding accuracy) by Eratosthenes during this time period. Eratosthenes knew that the Sun was directly overhead during the Summer solstice in the ancient Egyptian city Syene. Aware of the distance from Alexandria to Syene, he was able to approximate the Earth's circumference using trigonometry and the length of a shadow cast in Alexandria during the Summer solstice. His mathematics was sound; had Eratosthenes been working with accurate measurements, his estimate of the Earth's meridional circumference would have been nearly exact.

It is now known that the approximate shape of the Earth is an oblate spheroid. Because the Earth rotates, its spheroidal shape compresses at the poles and bulges at the equator. For convenience, we will stick with the assumption that the Earth is a sphere, but the same arguments can be applied if we acknowledge the oblate structure.

The Earth's equator is an example of a great circle. Two points that lie opposite each other on a great circle are said to be diametrically opposed (or antipodal points). Let $C$ be any one of the Earth's great circles. Let $\tau$ be a continuous function mapping each point on the Earth to the temperature at that point. We will generalize the above claim by arguing that some pair of diametrically opposed points $p,q$ on $C$ satisfy $\tau(p) = \tau(q)$.

To prove this claim, we will introduce a new function $\delta(p,q) = \tau(p) - \tau(q)$, defined for all pairs of diametrically opposed points $p,q$ on $C$. Starting with any pair of diametrically opposed points $p,q$, consider the value of $\delta(p,q)$. If $\delta(p,q) = 0$, we have found the desired pair of points since $\delta(p,q) = 0$ only if $\tau(p) = \tau(q)$. Otherwise, observe that $\delta(p,q)$ must take on the opposite sign of $\delta(q,p)$. However, we can move from $p$ along the great circle in a continuous manner, evaluating $\delta$ at all intermediate pairs of diametrically opposed points until we reach $q$. Since $\delta$ changes sign during this process, there must be some intermediate pair of points $p^*, q^*$  for which $\delta(p^*, q^*) = 0$. This argument follows by the continuity of $\delta$ and can be formalized with the intermediate value theorem. Furthermore, observe that the claim holds for any continuous function over the Earth's surface (like barometric pressure or altitude).

A shrewd reader may realize that the above argument can easily be extended to show that there are infinitely many pairs of diametrically opposed points on the Earth's surface with the same temperature. In fact, the Borsuk-Ulam theorem states that, for any continuous mapping $f$ from the sphere onto $R^2$,  there is some pair of diametrically opposed points on the sphere that $f$ maps to the same point in $R^2$. This result can be summarized as follows.

At any point in time, there are two antipodal points on the Earth's surface with the same temperature and barometric pressure.

This claim works for any continuous function mapping points on the Earth's surface to points in $R^2$. In fact, the theorem generalizes to higher dimensional spheres, but the two-dimensional version will suffice to prove the next claim.

Ham Sandwich Theorem. A ham and cheese sandwich can always be cut in half such that each half contains the same amount of bread, ham, and cheese. 

We will formalize this problem as follows. Let $B$, $H$, and  $C$ be bounded subsets of $R^3$ corresponding respectively to the bread, ham, and cheese. Our goal is to find a plane that bisects $B$, $H$, and  $C$ simultaneously.

Let $p$ be a point on the unit sphere embedded in $R^3$ centered at the origin. Consider the set of all planes parallel to the tangent plane at $p$. We will imagine these planes as being oriented in the direction of the normal vector from the origin to $p$. Thus, we can refer to points as being right of the plane or left of the plane. By the intermediate value theorem, one of these planes must bisect $B$. This follows since if we choose a far off plane in one direction, all of the bread will be left of the plane, and if we choose a far off plane in the opposite direction, all of the bread will be right of the plane.

We can therefore map every point $p$ on the sphere to a plane $\pi(p)$ that bisects $B$. Moreover, if we define $h(p)$ and $c(p)$ to be the amount of ham and cheese, respectively, right of the plane $\pi(p)$, then $f(p) = (h(p), c(p))$ is a continuous function from each point on the sphere to $R^2$. Indeed, we can always choose the plane $\pi(p)$ in an unambiguous manner (say, preferring the middle-most plane bisecting $H$) to guarantee continuity.

By the Borsuk-Ulam theorem, there exists two antipodal points $p$ and $q$ on the unit sphere for which $f(p) = f(q)$. However, since $p$ and $q$ are antipodal, it follows that $\pi(p) = \pi(q)$ (they have the same set of planes, and thus our choice of the middle-most plane is identical). But, since $\pi(p)$ and $\pi(q)$ are oriented in opposite directions, the fact that $f(p) = f(q)$ implies that $\pi(p)$ bisects both $H$ and $C$. This concludes the proof as $\pi(p)$ also bisects $B$ by definition.

As mentioned above, these results generalize to higher dimensions. We will leave it as an exercise to come up with some interesting four-dimensional example of the Ham Sandwich theorem. Be festive! It's Thanksgiving today in the United States, so try your best to imagine a four-dimensional turkey draped in four-dimensional cranberry sauce.

Permutation Statistics

In our previous post, we discussed the inconceivably large number of ways that $n$ numbers can be permuted. The magnitude of $n!$ for even reasonably small values of $n$ is nearly impossible to comprehend in any physical sense. To put things in a somewhat tangible perspective, consider the number $59! \approx 1.4 \times 10^{80}$.

If we employ some elementary stellar physics we can approximate the number of hydrogen atoms in a typical star at around $10^{57}$. Though incredibly large, we haven't come close to the measure of $59!$. A typical galaxy, like the one we call home, has around 400 billion stars. Basic arithmetic then reveals that such a galaxy has around $4 \times 10^{68}$ hydrogen atoms, still meager when compared to $59!$. Estimating the number of galaxies in the observable universe at around 80 billion, we can approximate the number of observable hydrogen atoms in the universe at $~3.2 \times 10^{79}$, which constitutes ~74% of all (baryonic) matter. Only after considering all atoms in the observable universe can we find a physical comparison to $59!$. One seeking quantities analogous to larger factorials will quickly run out of universe.

Despite the apparent complexity of enumerating permutations, mathematics provides a means to make precise universal statements about their properties. We discovered in our previous post that the fraction of permutations that are derangements converges to $1/e$ as $n$ tends to $\infty$. In another post, we learned about the distribution of cycles in permutations. In particular, we discovered that the expected number of cycles in a permutation converges to the $n$-th harmonic number $H_n$ as $n$ tends to $\infty$. In today's post, we will extend our list of interesting permutation statistics by exploring the notion of order.

When dealt a hand in a card game, it is common to arrange the cards in one's hand in a particular order. By comparing the rank of two cards (breaking ties by comparing the suits in alphabetical order), one can always arrange cards into their unique sorted order. This process of sorting is a fundamental concept in computer science, and a number of algorithms exist for sorting a set of $n$ elements. Before discussing any such sorting algorithms, we will first endeavor to get an idea of the extent to which a set of $n$ elements can be disordered.

The numbers $1,2,\dots,n$ serve not only as being pairwise distinct elements but also provide an implicit order $1 < 2 < \dots < n$. This order allows us to conveniently measure order-related statistics of random permutations. For instance, what is the expected number of elements that are already in their sorted position in a uniformly random permutation $\pi$ of $1,2,\dots,n$? We can compute this expectation as follows.

Define $X_i$ to be an indicator variable that is $1$ if $i$ is mapped to position $i$ by $\pi$ and $0$ otherwise. Then, the desired expectation can be expressed as
\[ E\left[\sum_{i = 1}^n X_i \right] \] which by linearity of expectation simplifies to
\[ \sum_{i = 1}^n E[X_i]. \] As $E[X_i] = P(X_i = 1) = 1/n$, it follows that on average $1$ element is mapped to its own position.

Another key measure of disorder is the number of inversions. An inversion in a permutation is a pair $i < j$ where $i$ occurs at a later position than $j$ (the two elements are out of order). What is the expected number of inversions in a uniformly random permutation $\pi$ of $1,2,\dots,n$?

Define $X_{i,j}$ to be an indicator variable that is $1$ if $i$ and $j$ form an inversion in $\pi$ and $0$ otherwise. Then, our expectation reduces to
\[ \sum_{i \neq j}P(X_{i,j} = 1) \] by linearity of expectation. Since $i$ and $j$ are in one of their two possible relative orders with equal probability, the expectation is thus $\frac{1}{2} {n \choose 2}$.

Let's consider another measure of sortedness. Suppose that we were to partition the numbers in a permutation into contiguous sorted subsequences. For example, the sorted subsequences for the permutation $1,6,7,3,4,5,2,8$ are $(1,6,7)$, $(3,4,5)$, and $(2,8)$. In this example, the permutation is composed of $3$ sorted subsequences. How many subsequences would one expect for a uniformly random permutation $\pi$ of $1,2,\dots,n$?

Observe that each sorted subsequence, with the exception of the first one, begins with a number that is smaller than its predecessor. Moreover, any such number must always start a new increasing subsequence. Thus, if we define $X$ to be the number of consecutive pairs $a,b$ where $a > b$, it follows that the desired expectation can be computed as
\[ 1 + E[X] = 1 + \sum_{i=1}^{n-1} E[X_i] \] where $X_i$ is $1$ if the number in position $i$ is larger than the number in position $i+1$ and $0$ otherwise. Since $E[X_i] = P(X_i = 1) = 1/2$, the desired expectation is $\frac{1}{2}(n+1)$.

The previous result should not be surprising because of the symmetry of increasing subsequences and decreasing subsequences. That is, each number in a permutation must either start an increasing subsequence or a decreasing subseqeuence, with the exception of the first number which starts both an increasing and decreasing subsequence. Thus, if $X$ is the number of increasing subsequences and $Y$ is the number of decreasing subsequences, $X + Y = n + 1$. By linearity of expectation, we can then conclude that
\[ E[X] = E[Y] = \frac{1}{2}(n + 1) \] since $E[X]$ must equal $E[Y]$ by symmetry.

By applying these straightforward techniques, we can discern a number of properties regarding the order of elements in a permutation. The next expectation we consider turns out to be a little more involved.

Let's pursue further this notion of increasing and decreasing subsequences. Suppose that we partitioned $\pi$ into contiguous subsequences that can be either increasing or decreasing. We will create this partition in a way that minimizes the number of parts as follows. Look at the first two numbers. If they are increasing, start building up an increasing subsequence. If they are decreasing, start building up a decreasing subsequence. When our subsequence cannot be extended any further, start over using the subsequent two numbers. For example, the subsequences for the permutation $9,5,1,6,10,2,8,7,3,4$ would be $(9,5,1)$, $(6, 10)$, $(2,8)$, $(7,3)$, and $(4)$. How many subsequences would one expect in such a partition for a uniformly random permutation $\pi$ of $1,2,\dots,n$?

Let $a, b, c$ be a consecutive subsequence in the permutation $\pi$. We say that $b$ is an extremal point if $b > a,c$ or $b < a,c$. A subsequence of $\pi$ of size $k>2$ is said to be alternating if it contains $k-2$ extremal points. For example, in the permutation $9,5,1,6,10,2,8,7,3,4$:

• 1, 10, 2, 8, and 3 are the extremal points, and
• (5,1,6), (6,10,2), (10,2,8), (2,8,7), (6,10,2,8), (10,2,8,7), (6,10,2,8,7), and (7,3,4) are the alternating subsequences.

For $k = 3,4,\dots,n$, let $X_k$ be the number of alternating subsequences in $\pi$ of size $k$. Let $X_{k,i}$ be an indicator variable that is $1$ if the subsequence of size $k$ starting at position $i$ is alternating and $0$ otherwise. Observe that

\[ X_k = \sum_{i=1}^{n-k+1} X_{k,i} \]

and therefore

\[ E[X_k] = \sum_{i=1}^{n-k+1} E[X_{k,i}] \]

by linearity of expectation. Let $\phi(k)$ be the number of ways of permuting $k$ numbers into an alternating sequence. We can then express $P(X_{k,i} = 1)$ as $\frac{1}{k!}\phi(k)$ from which it follows that

\[ E[X_k] = \frac{n-k+1}{k!}\phi(k)\]

since $E[X_{k,i}] = P(X_{k,i} = 1)$.

We can relate alternating subsequences to the number of increasing and decreasing subsequences in the following manner. Observe that with the exception of the first subsequence, the start of every increasing or decreasing subsequence follows an extremal point. Thus, if we define $X$ to be the number of subsequences in our partition, we can estimate $X \approx 1 + X_3$. However, suppose that $\pi$ contained an alternating subsequence of size $4$. It could have been that only one of the two extremal points in this alternating subsequence was followed by a new increasing or decreasing subsequence. Thus, we can refine our approximation by discounting all alternating subsequences of size $4$. That is, $X \approx 1 + X_3 - X_4$. This estimation goes awry whenever an alternating subsequence of size $4$ is actually part of an alternating subsequence of size $5$, in which case we would have discounted 1 too many subsequences. We can thus refine the approximation further as $X \approx 1 + X_3 - X_4 + X_5$. By the inclusion-exclusion principle, we can extend this reasoning to achieve the complete relation
\[X = 1 + \sum_{k=3}^n (-1)^{n-1} X_k \] from which the desired expectation can be computed as
\[E[X] = 1 + \sum_{k=3}^n (-1)^{n-1} \frac{n - k + 1}{k!}\phi(k). \]
The Taylor series for the function $2(\tan{x} - \sec{x})$ about the point $0$ is
\[-\phi(0) + \phi(1)x - \phi(2)\frac{x^2}{2!} + \phi(3)\frac{x^3}{3!} - \dots \] if we define $\phi(0) = \phi(1) = 1$. Observe the similarity that this expansion has with $E[X]$. We can relate the two with the identity
\[ E[X] = 1 + (n+1)(2\tan(1) - 2\sec(1) + 1) - \left(1 + \frac{d}{dx}\Biggl| 2(\tan{x} - \sec{x})\Biggr|_{x=1}\right) \] from which it follows that
\[ E[X] \sim (2\tan(1) - 2\sec(1) + 1)n \] as $n \to \infty$. Thus, we have shown that the expected number of increasing and decreasing subsequences converges to about $0.4132n$ as $n$ tends to $\infty$.

Beyond the Riffle

Our two previous posts illustrated how employing randomness and estimating probabilities can uncover surprisingly effective strategies for games. In both cases, we analyzed statistics of uniformly random permutations. We have yet to give a proper definition of a uniformly random permutation and explain whether or not one can be generated algorithmically. Today's post will rectify this shortcoming and give  another example of a game that relates to random permutations.

The number of ways $n$ distinct elements can be arranged into a linear order is $n!$. Each of these arrangements defines a unique permutation of the $n$ elements.  A uniformly random permutation is simply a random variable that takes on one of these $n!$ permutations, each with an equal probability. The growth rate of $n!$ is incredibly fast, as may be more apparent by Stirling's approximation
\[n! \sim \sqrt{2\pi n} \left( \frac{n}{e} \right)^n. \] Thus, it seems reasonable to ask whether a uniformly random permutation can actually be generated in practice.

Anyone familiar with playing cards will likely know a few different techniques for shuffling a deck. One of the most commonly used techniques is the riffle, but how effective is it? If one's goal is to have the cards in a uniformly random order, then the riffle is not very effective on its own (consider how likely it is that the card starting at the bottom of the deck ends up at the top). However, by properly formulating these concepts, the mathematician Persi Diaconis was able to prove that 7 riffles is sufficient for most games.

From a computational perspective, there turns out to be a very simple technique for generating a uniformly random permutation called the Fisher-Yates shuffle. This technique was popularized by the eminent computer scientist Donald Knuth, and he described the technique in detail in Volume 2 of his epic monograph The Art of Computer Programming. The technique is illustrated in the following code snippet:

# To shuffle a list A of n elements (A[1],...,A[n])
for i in 1..n do
    j = random from i,i+1,...,n
    swap A[i] and A[j]

Those familiar with computer science will notice that this algorithm has several desirable qualities. For example, the amount of auxiliary space required is small even when A is very large. Furthermore, the algorithm will run to completion quickly. In particular, the Fisher-Yates shuffle is an example of a linear time algorithm since the amount of computation performed is $O(n)$ for a list of size $n$.

We will now consider a game, wherein the problem is not about surviving (like in our previous posts) but instead about reducing the amount of time it takes to perform an action. This notion of computation time will be discussed in more detail in future posts, but for now it will suffice to defer to one's intuition.

A Secret Santa is a game/tradition often played during Christmas in western cultures. Each player is randomly assigned a unique person to whom they must anonymously give a gift. No two people can be assigned the same person, and no one person can be assigned themselves. How can one randomly sample among all valid assignments so that each is chosen with equal probability?

Observe that every valid assignment corresponds to a permutation. However, the converse is not true. In a permutation, a number can be mapped back to its own position, resulting in an invalid assignment. A permutation in which no number maps to its own position is called a derangement. We can therefore generate a Secret Santa assignment as follows:

1. Generate an assignment from a uniformly random permutation using the Fisher-Yates shuffle.
2. Repeat the previous step until no person is assigned to themselves.

The final assignment we end up with will be a uniformly random derangement since we consider all possible assignments with equal probability in step (1). We will conclude the discussion by considering how long this procedure takes to complete.

Our assignment procedure is an example of a randomized algorithm. In particular, the amount of time it takes for the procedure to complete is not deterministic. Thus, we need to treat this runtime as a random variable, and in particular, we would like to know the expectation of this random variable; that is, we want to compute the expected runtime of the algorithm.

Let $p$ be the probability that a uniformly random permutation is a derangement. In a given iteration, our algorithm will therefore complete with probability $p$ and continue with probability $1-p$. Thus, we can think of the algorithm as a sequence of independent trials with success probability $p$, where the runtime is given by the number of trials before the first success. That is, the runtime is given by a geometric distribution, which has expectation $1/p$. We can therefore complete the analysis by estimating $p$.

For a uniformly random permutation $\pi$, let $A_i$ be the event that $i$ is mapped to its own position for $i=1,\dots,n$. The probability that $\pi$ is a derangement can therefore be expressed as $P(\overline{A_1} \cap \overline{A_2} \cap \dots \cap \overline{A_n})$. Observe that these events are not independent. The probability $P(\overline{A_i})$ is simply $(1 - 1/n)$ since $i$ has a $1/n$ chance of being mapped to its own position. However, we can argue that $P(\overline{A_i} | \overline{A_1} \cap \dots \cap \overline{A_{i-1}}) \geq P(\overline{A_i})$ since knowing that none of the first $i-1$ elements mapped to their own positions can only decrease the likelihood that $i$ maps to its own position. Thus, we can proceed to bound $p$ from below as
\[ P(\overline{A_1} \cap \overline{A_2} \cap \dots \cap \overline{A_n}) \geq P(\overline{A_1})P(\overline{A_2})\cdots P(\overline{A_n}), \] the right-hand side of which equates to $(1 - 1/n)^n$. Using the definition
\[e^x = \lim_{n \to \infty} \left( 1 + \frac{x}{n} \right)^n \] it follows that $p \geq 1/e$ as $n \to \infty$.

We have not yet made any claim to how accurate this estimate is, but rest assured that this (yet another) surprise appearance of the illustrious $e$ is no coincidence. To better bound this estimate we will employ the inclusion-exclusion principle. The argument goes as follows.

Suppose we start with the trivial approximation that all permutations are derangements. This approximations gives the crude estimate $p \approx 1$.  We can improve this by discounting all permutations in which $i$ occurs in its own position for $i = 1,\dots,n$. That is, we can estimate
\[ p \approx 1 - \sum_{i=1}^n \frac{1}{n} \] since $i$ occurs in its own position with probability $1/n$. This approximation gives the slightly less crude estimate $p = 0$. The error in this approximation is that we double counted. Permutations in which distinct $i$ and $j$ both occurred in their own positions where discounted twice, once for $i$ and once for $j$. Thus, we can improve our approximation by adding back these permutations, giving the estimate
\[ p \approx 1 - 1 + \sum_{1 \leq i < j \leq  n} \frac{1}{n(n-1)} \] since the probability that distinct $i$ and $j$ both occur in their own positions is $1/(n(n-1))$. Computing the summation gives the slightly better estimate $p=1/2$. The error in this approximation is again a form of double counting. If all distinct $i$, $j$, and $k$ occurred in their own positions, we would have added them back twice (instead of once). Thus, we can repeat the argument to improve the estimate to
\[ p \approx 1 - 1 + 1/2 - \sum_{1 \leq i < j < k \leq n} \frac{1}{n(n-1)(n-2)} \] since the probability that distinct $i$, $j$, and $k$ occur in their own positions is $1/(n(n-1)(n-2))$. Computing this summation gives the improved estimate $p = 1/3$. If we continue this reasoning, eventually our summation will terminate with the $n$-th estimate, giving the exact probability
\[ p = \sum_{k=0}^n \frac{(-1)^k}{k!}. \] This summation is the first $n$ terms of the Taylor series for the exponential function $e^x$ evaluated at $x=-1$. Thus, we can conclude that as $n \to \infty$ $p \to 1/e$. Hence, the simple trial and error approach to generating a uniformly random derangement takes only $e=2.7182818...$ iterations on average. Not too shabby.

We leave you with a straightforward exercise:

Using Stirling's approximation and estimates on how often people play card games, show that no two truly random decks will ever, in human history, be the same (except with an inconceivably low probability).

The Prisoners' Gambit

In our last post, we discussed the notion of randomness and how the perception of it has undergone a facelift in recent decades. Having once been thought of as an unruly impediment, randomness is now understood to provide astounding utility towards solving problems. In today's post, we continue along this theme by discussing another game in which randomness plays a vital role.

In the riddleverse, prisoners escape their forlorn lives to become the subject of many interesting and challenging puzzles. The reasoning involved in these puzzles often features a wide range of mathematical topics. For example, the Three Prisoners Problem considers a classic paradox in probability theory akin to Betrand's Box Paradox or the Monty Hall Problem. The Prisoners and Hats Puzzle delves into aspects of inductive reasoning. Likewise, anyone familiar with game theory has most likely heard of the Prisoner's Dilemma.

In an attempt to further demonstrate the power of randomness, we consider the following prisoner-themed puzzle.

A prison warden has decided to subject 100 prisoners to a game. The warden begins by shuffling the names of the prisoners into 100 urns, one name to one urn. One at a time, the prisoners are let into the room with the urns to attempt to locate their own name. Each prisoner is allowed to look inside 50 urns. If any one prisoner fails to find the urn with his or her name after the 50 guesses, all prisoners are immediately executed. However, if each prisoner finds his or her own name, they are all set free. The prisoners are allowed to strategize ahead of time, but after the game begins they cannot communicate in any way (they cannot mark the urns or move the names around between urns). If each prisoner guesses 50 random urns, they survive with probability $2^{-100} \approx 0$. However, the clever prisoners realize a strategy with an ~30% chance of survival — what is the strategy?

Let's begin by formalizing the statement of the problem. Suppose that the prisoners are named $1,2,\dots,100$. Let $x_1, x_2, \dots, x_{100}$ represent the 100 urns. Once the names of the prisoners are shuffled into the urns, we can think of $x_i$ as being representative of the name that was assigned to the $i$-th urn. In other words, $x_1, x_2, \dots, x_{100}$ corresponds to a uniformly random permutation of the numbers $1,2,\dots,100$.

When the $i$-th prisoner enters the room, they are allowed to choose 50 urns, one of which must contain name $i$. The first prisoner knows nothing about the order of the names in the urns other than that the order is uniformly random. Thus, this prisoner's chance of success is 1/2, regardless of which 50 urns were chosen. If the same were true for the second prisoner, the chance of them both finding their own names reduces to $1/4$, which is already less that the purported ~30% success rate!

If you haven't heard of this problem before, spend a few moments trying to come up with a good strategy. You might begin to doubt the existence of a strategy with an ~30% success rate, or you might think that any such strategy involves bending the rules. No rule bending is necessary.

The key to this problem lies in an understanding of uniformly random permutations. Suppose that we had just 6 prisoners and that their names were arranged into the urns in the order $6,1,5,4,3,2$.

An example assignment of the prisoners' names into 6 urns. 

Observe that $6$ is in the first urn, which means that some other name is in the sixth urn. Indeed, $2$ is in the sixth urn, which means that the second urn is occupied by another distinct name. Looking at the second urn, we find $1$, which completes the cycle as the first urn was already known to be occupied by $6$. In general, we can apply this reasoning starting from any urn, and eventually, we will end up back where we started. It follows then that any permutation can be decomposed into a set of cycles.

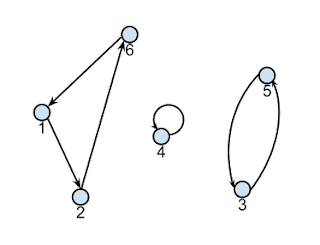The cycle decomposition of the permutation 6,1,5,4,3,2.

This decomposition leads to the following strategy. Suppose that prisoner $1$ starts by looking inside the first urn. If he uncovers his name, he has succeeded, so let's assume he has uncovered some other name $j$. He then looks inside the $j$-th urn, again succeeding if he finds his own name. Assuming otherwise, he will have uncovered some other name $k$. He then proceeds to look inside the $k$-th urn, repeating this process until he uncovers his own name. As illustrated above, he must eventually loop back to the first urn, which happens only once he has uncovered his own name. Thus, if the cycle traversed by the prisoner has size at most 50, he is guaranteed to find his name within 50 guesses. If each prisoner $i$ performs the same procedure, starting from the $i$-th urn, then all prisoners will succeed if and only if all cycles are of size at most 50.

To complete the analysis of this strategy, we consider how often every cycle has size at most 50 in the cycle decomposition of a uniformly random permutation. The goal is to prove that this bound is achieved ~30% of the time. For added generality, we will analyze permutations of $n$ numbers.

Let $\pi$ be sampled uniformly at random over all permutations of $1,2,\dots,n$. Let $G=(V,E)$ be a graph corresponding to the cycle decomposition of $\pi$. We want to compute the probability that all cycles in $G$ have size at most $n/2$. Let $X$ be a random variable for the number of cycles of size greater than $n/2$. Then, the desired probability is $P(X = 0)$. Let $X_C$ be an indicator variable such that

• $X_C = 1$ if $C$ is a cycle in $G$, and
• $X_C = 0$ otherwise.

We can therefore conclude that
\[ X = \sum_{C \subseteq V, |C| > n/2} X_C. \] Observe that $X$ itself is an indicator variable since you can have at most one cycle of size greater than $n/2$. Thus, $P(X = 0) = 1 - E[X]$. From the above equation it follows that
\[ E[X] = E\left[\sum_{C \subseteq V, |C| > n/2} X_C\right], \] which by linearity of expectation simplifies to
\[ E[X] = \sum_{C \subseteq V, |C| > n/2} E[X_C], \] which can be rewritten as
\[ E[X] = \sum_{k>n/2} \sum_{C \subseteq V, |C| = k} P(X_C=1), \] since $E[X_C] = P(X_C = 1)$. We thus need to compute the probability that a given set of $k$ vertices form a cycle in $G$. This event happens if and only if the $k$ corresponding numbers are themselves a cyclic permutation within $\pi$. This event happens with probability $1 / \left( k {n \choose k} \right)$. Thus, we can compute the desired expectation as
\[ E[X] = \sum_{k>n/2} \sum_{C \subseteq V, |C| = k} \frac{1}{k{n \choose k}}, \] and since there are ${n \choose k}$ subsets of $V$ of size $k$, we conclude that
\[ E[X] = \sum_{k=n/2 + 1}^n \frac{1}{k}. \] This series should look familiar from our last post. The sum of the series $\sum_{h=1}^i\frac{1}{h}$ is the $i$-th harmonic number $H_i$, and we can therefore write our expectation as
\[ E[X] = H_n - H_{n/2}.\] By approximating the harmonic numbers, we conclude that
\[ E[X] \leq \ln{n} - \ln{\left(n/2\right)} = \ln{2},\] and thus,
\[ P(X = 0) \geq 1 - \ln(2) \approx  0.306852819...\] which completes the analysis.

Note that we have proven something slightly more general. So long as $n$ prisoners are given at least $n/2$ guesses each, their probability of success is ~30%. What's more is that if the prisoners are given at least $\sqrt{1/e}n \approx 0.607n$ guesses, their survival rate exceeds 50%. This is an astounding improvement over the naive solution of having each prisoner choose urns at random.

Can you do better? If not, can you prove a matching lower bound?

A Game of Chance

Throughout human history, randomness has been a bane to everyday life. Imagine the vicissitude a farmer endures managing the randomness of meteorological processes. Were it not for the predictable and seemingly deterministic structure of large-scale systems and the resultant diurnal and seasonal patterns, a farmer's way of life would not be feasible. The same reasoning can be applied to many other professions vital to the advancement of human civilization.

The word random connotes unsettling notions of uncertainty and disorder. These ideas seem on the surface to be contrary to the methodical, systematic, and definite nature of mathematics. Paradoxically, it is through mathematics – via the study of probability theory – that randomness is best understood.

The inception of probability theory is often attributed to the mathematicians Pierre de Fermat and Blaise Pascal. But, Gerolamo Cardano seems to have been the first to rigorously analyze randomness from a mathematical perspective. Cardano made large contributions to algebra, being the first to publish solutions to cubic and quartic equations. He was also an accomplished gambler. In 1526, he wrote a book about games of chance, in which he discussed decision making when faced with randomness.

The pioneering work of Cardano and subsequent developments in probability theory marked the beginning of a new perspective on randomness. What was previously intractable became a science. And, with the advent of quantum mechanics, we have learned that randomness is not the result of a lack of understanding but a necessary and fundamental component of our universe.

In the past few decades, the story on randomness has taken an even more alarming turn. Randomized algorithms have demonstrated that randomness is not only something we can reason about but something we can leverage to solve problems. If you want to test if a number is prime, it helps to flip coins. In this vein, we discuss a game in which randomness is not only relevant but vital to any effective strategy.

Consider the following variant of the popular game show Deal or No Deal:

You are presented with n briefcases. Each briefcase contains an unknown quantity of money. The rules are as follows. You are allowed to select one briefcase at a time. Upon selecting a briefcase, its contents are revealed to you. You can then choose whether to keep the contents of this briefcase or reject it in favor of a future briefcase. Once you reject a briefcase, you cannot claim its contents anymore. Your goal is to choose the briefcase with the biggest payout. 

If we employ any deterministic strategy, an adversary (aware of our strategy) could arrange the briefcases in such a way that we would always choose the briefcase with the lowest payout. On the other hand, by employing randomness, a trivial strategy yields a success rate of at least $1/4$. That is, with probability $1/4$, we will choose the briefcase with the biggest payout.

Consider the following approach. First, permute the briefcases into a uniformly random order $b_1, b_2, \dots, b_n$. Then, select the first $n/2$ briefcases, rejecting them outright. Proceed through the remaining briefcases until we uncover one that yields a larger payout than any previously seen. If we uncover such a briefcase, keep it (otherwise, we can just "try out luck" with $b_n$).

Observe that this strategy will always win if the briefcase with the second largest payout was in the first half and the briefcase with the best payout was in the second half. Since the briefcases were arranged into a uniformly random permutation, this winning scenario happens at least $1/4$ of the time.

As we uncover a briefcase, say $b_i$, we can compute the probability that this briefcase is the best. This probability is

• $i/n$ if $b_i > b_j$, for all $j < i$, and
• $0$ otherwise.

Thus, the previously mentioned strategy can be restated as follows: Stop at the first briefcase with probability at least $1/2$ of being the best.

This raises the following questions:

1. What is the actual success rate of this strategy?
2.  Does there exist a similar strategy with a better success rate if we replace $1/2$ with some other threshold probability, say $p$? 

The answer to (2) is a definitive yes, and the optimal value of $p$ may seem surprising. It turns out that for large enough $n$, your best bet is to set $p = 1/e$, where $e = 2.71828...$  is Euler's number. The analysis is as follows.

As stated above, if $b_i$ is larger than all previously seen briefcases, it is the largest with probability $i/n$. Indeed, the largest briefcase had an $i/n$ chance of being in this range. Thus, for a given threshold probability $p$, our algorithm will stop at the first such $b_i$ encountered after position $k=\lfloor pn \rfloor$. Thus, the probability of success can be reduced to the probability that the first such $b_i$ encountered after position $k$ is also the largest briefcase. For $i  \geq k$, define

• $A_i$ to be the event that $b_i$ is the largest briefcase, and
• $B_i$ to be the event that the largest $b_j$ in $b_1,b_2,\dots,b_i$ satisfies $j \leq k$.

Then the desired probability can be calculated as
\[ \sum_{i=k+1}^n P(A_i) P(B_{i-1}) = \sum_{i=k+1}^n \frac{1}{n}\frac{k}{i-1} \] which can be simplified to
\[ \frac{k}{n}\sum_{i=k}^{n-1} \frac{1}{i} = \frac{k}{n}(H_{n-1} - H_{k-1}) \] where $H_j$ denotes the sum of the harmonic series from $1$ to $j$. Thus, for fixed threshold probability $p$ and $n \to \infty$, the success rate converges to
\[ \frac{k}{n}\ln{\left(\frac{n}{k}\right)} \sim -p\ln{p} \]
by using the approximation $H_j \sim \ln{j} + \gamma$, where $\gamma$ is the Euler–Mascheroni constant. To answer question (1) from above, we substitute $p = 1/2$ into this equation, giving a success rate of $1/2\ln{2} = 0.346573...$. By applying elementary calculus, the success rate can be shown to be largest when $p=1/e$; that is, the optimal threshold probability is $1/e$, which gives a success rate of $1/e = 0.367879...$.

We conclude with the following question: Can you do better?