In the riddleverse, prisoners escape their forlorn lives to become the subject of many interesting and challenging puzzles. The reasoning involved in these puzzles often features a wide range of mathematical topics. For example, the Three Prisoners Problem considers a classic paradox in probability theory akin to Betrand's Box Paradox or the Monty Hall Problem. The Prisoners and Hats Puzzle delves into aspects of inductive reasoning. Likewise, anyone familiar with game theory has most likely heard of the Prisoner's Dilemma.
In an attempt to further demonstrate the power of randomness, we consider the following prisoner-themed puzzle.
A prison warden has decided to subject 100 prisoners to a game. The warden begins by shuffling the names of the prisoners into 100 urns, one name to one urn. One at a time, the prisoners are let into the room with the urns to attempt to locate their own name. Each prisoner is allowed to look inside 50 urns. If any one prisoner fails to find the urn with his or her name after the 50 guesses, all prisoners are immediately executed. However, if each prisoner finds his or her own name, they are all set free. The prisoners are allowed to strategize ahead of time, but after the game begins they cannot communicate in any way (they cannot mark the urns or move the names around between urns). If each prisoner guesses 50 random urns, they survive with probability $2^{-100} \approx 0$. However, the clever prisoners realize a strategy with an ~30% chance of survival — what is the strategy?
Let's begin by formalizing the statement of the problem. Suppose that the prisoners are named $1,2,\dots,100$. Let $x_1, x_2, \dots, x_{100}$ represent the 100 urns. Once the names of the prisoners are shuffled into the urns, we can think of $x_i$ as being representative of the name that was assigned to the $i$-th urn. In other words, $x_1, x_2, \dots, x_{100}$ corresponds to a uniformly random permutation of the numbers $1,2,\dots,100$.
When the $i$-th prisoner enters the room, they are allowed to choose 50 urns, one of which must contain name $i$. The first prisoner knows nothing about the order of the names in the urns other than that the order is uniformly random. Thus, this prisoner's chance of success is 1/2, regardless of which 50 urns were chosen. If the same were true for the second prisoner, the chance of them both finding their own names reduces to $1/4$, which is already less that the purported ~30% success rate!
If you haven't heard of this problem before, spend a few moments trying to come up with a good strategy. You might begin to doubt the existence of a strategy with an ~30% success rate, or you might think that any such strategy involves bending the rules. No rule bending is necessary.
The key to this problem lies in an understanding of uniformly random permutations. Suppose that we had just 6 prisoners and that their names were arranged into the urns in the order $6,1,5,4,3,2$.
 |
| An example assignment of the prisoners' names into 6 urns. |
Observe that $6$ is in the first urn, which means that some other name is in the sixth urn. Indeed, $2$ is in the sixth urn, which means that the second urn is occupied by another distinct name. Looking at the second urn, we find $1$, which completes the cycle as the first urn was already known to be occupied by $6$. In general, we can apply this reasoning starting from any urn, and eventually, we will end up back where we started. It follows then that any permutation can be decomposed into a set of cycles.
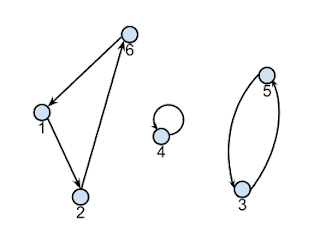 |
| The cycle decomposition of the permutation 6,1,5,4,3,2. |
This decomposition leads to the following strategy. Suppose that prisoner $1$ starts by looking inside the first urn. If he uncovers his name, he has succeeded, so let's assume he has uncovered some other name $j$. He then looks inside the $j$-th urn, again succeeding if he finds his own name. Assuming otherwise, he will have uncovered some other name $k$. He then proceeds to look inside the $k$-th urn, repeating this process until he uncovers his own name. As illustrated above, he must eventually loop back to the first urn, which happens only once he has uncovered his own name. Thus, if the cycle traversed by the prisoner has size at most 50, he is guaranteed to find his name within 50 guesses. If each prisoner $i$ performs the same procedure, starting from the $i$-th urn, then all prisoners will succeed if and only if all cycles are of size at most 50.
To complete the analysis of this strategy, we consider how often every cycle has size at most 50 in the cycle decomposition of a uniformly random permutation. The goal is to prove that this bound is achieved ~30% of the time. For added generality, we will analyze permutations of $n$ numbers.
Let $\pi$ be sampled uniformly at random over all permutations of $1,2,\dots,n$. Let $G=(V,E)$ be a graph corresponding to the cycle decomposition of $\pi$. We want to compute the probability that all cycles in $G$ have size at most $n/2$. Let $X$ be a random variable for the number of cycles of size greater than $n/2$. Then, the desired probability is $P(X = 0)$. Let $X_C$ be an indicator variable such that
- $X_C = 1$ if $C$ is a cycle in $G$, and
- $X_C = 0$ otherwise.
\[ X = \sum_{C \subseteq V, |C| > n/2} X_C. \] Observe that $X$ itself is an indicator variable since you can have at most one cycle of size greater than $n/2$. Thus, $P(X = 0) = 1 - E[X]$. From the above equation it follows that
\[ E[X] = E\left[\sum_{C \subseteq V, |C| > n/2} X_C\right], \] which by linearity of expectation simplifies to
\[ E[X] = \sum_{C \subseteq V, |C| > n/2} E[X_C], \] which can be rewritten as
\[ E[X] = \sum_{k>n/2} \sum_{C \subseteq V, |C| = k} P(X_C=1), \] since $E[X_C] = P(X_C = 1)$. We thus need to compute the probability that a given set of $k$ vertices form a cycle in $G$. This event happens if and only if the $k$ corresponding numbers are themselves a cyclic permutation within $\pi$. This event happens with probability $1 / \left( k {n \choose k} \right)$. Thus, we can compute the desired expectation as
\[ E[X] = \sum_{k>n/2} \sum_{C \subseteq V, |C| = k} \frac{1}{k{n \choose k}}, \] and since there are ${n \choose k}$ subsets of $V$ of size $k$, we conclude that
\[ E[X] = \sum_{k=n/2 + 1}^n \frac{1}{k}. \] This series should look familiar from our last post. The sum of the series $\sum_{h=1}^i\frac{1}{h}$ is the $i$-th harmonic number $H_i$, and we can therefore write our expectation as
\[ E[X] = H_n - H_{n/2}.\] By approximating the harmonic numbers, we conclude that
\[ E[X] \leq \ln{n} - \ln{\left(n/2\right)} = \ln{2},\] and thus,
\[ P(X = 0) \geq 1 - \ln(2) \approx 0.306852819...\] which completes the analysis.
Note that we have proven something slightly more general. So long as $n$ prisoners are given at least $n/2$ guesses each, their probability of success is ~30%. What's more is that if the prisoners are given at least $\sqrt{1/e}n \approx 0.607n$ guesses, their survival rate exceeds 50%. This is an astounding improvement over the naive solution of having each prisoner choose urns at random.
Can you do better? If not, can you prove a matching lower bound?
No comments :
Post a Comment